Case Study: Three State Synchronous Counter

Introduction

A synchronous machine is one where all flip flops are hooked up to the same clock.

If you model behavior using a Mealy or Moore machine, and follow the steps for implementing it, you get synchronous sequential circuits.

We're going to implement a synchronous counter. We contrast this synchronous counter with a asynchronous counter (a counter where all flip flops were not hooked to the same clock. This was discussed in another set of notes.

This is an unusual counter. Normally, if you have a standard up-counter, it counts up starting from (0)^k (zero, repeated k times), all the up way to (1)^k (one, repeated k times), and then starts back at (0)^k and counts up again. (We could implement a down counter than counts backwards, too).

However, there's no reason we can't implement a counter that counts 00, 01, 10, and then back to 00. There might be no reason why we should do so, either.

Nevertheless, since we can implement an up-counter of this kind let's do so. It's a good exercise.

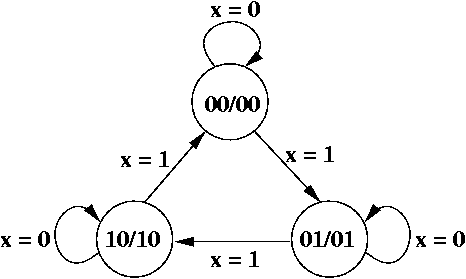
Here's the 3-state up counter, as a Moore machine.

Starting Out

First, we fill out the state variables and the input variables. Those serve as the state transition table inputs.

Row	q₁	q₀	x
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

Then the Outputs (for a Moore machine)

Since this is a Moore machine, we should fill out the outputs next. We look at the state (the value left of the slash in 00/00) and fill out the corresponding output (the value right of the slash in 00/00).

For counters, it's almost always the case that the state label and the outputs are identical.

Row	q₁	q₀	x	q₁⁺	q₀⁺	z₁	z₀
0	0	0	0			0	0
1	0	0	1			0	0
2	0	1	0			0	1
3	0	1	1			0	1
4	1	0	0			1	0
5	1	0	1			1	0
6	1	1	0			d	d
7	1	1	1			d	d

They aren't completely identical because there is no state 11. We always place d (don't cares) in the rows of states that don't exist.

Then the Next States

This is easy for a counter. When the input is a 0, then the state doesn't change. When it's a 1, it increments.

Row	q₁	q₀	x	q₁⁺	q₀⁺	z₁	z₀
0	0	0	0	0	0	0	0
1	0	0	1	0	1	0	0
2	0	1	0	0	1	0	1
3	0	1	1	1	0	0	1
4	1	0	0	1	0	1	0
5	1	0	1	0	0	1	0
6	1	1	0	d	d	d	d
7	1	1	1	d	d	d	d

Picking Flip Flops

Let's make life simple and pick D flip flops. That means we simply copy the column q₁⁺ to D₁ and q₀⁺ to D₀.

Row	q₁	q₀	x	q₁⁺	q₀⁺	z₁	z₀	D₁	D₀
0	0	0	0	0	0	0	0	0	0
1	0	0	1	0	1	0	0	0	1
2	0	1	0	0	1	0	1	0	1
3	0	1	1	1	0	0	1	1	0
4	1	0	0	1	0	1	0	1	0
5	1	0	1	0	0	1	0	0	0
6	1	1	0	d	d	d	d	d	d
7	1	1	1	d	d	d	d	d	d

Drawing the Circuit

Then, drawing out the circuit.

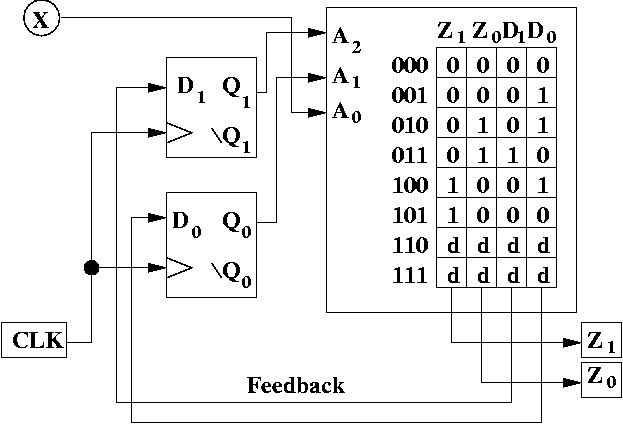
This basically consists of drawing the ROM correctly. The main mistakes that you're like to make is: copying columns incorrectly, adding more columns than the outputs and the flip flops control, failing to label the address bits and the addresses.

It's a good idea, when you draw the circuit to compare your version to the one here, and ask "What did I leave out?"

Summary

An up-counter usually has two operations. Counting up and holding. You can also have counters that don't count all 2^k values but only count some of it, as in the example above.

What the above exercise should illustrate is that once you can model something using a Moore or Mealy machine, it's straight-forward to implement afterwards. There is a mechanical process, which you practice, and it becomes easy after doing it a few times.

Web Accessibility