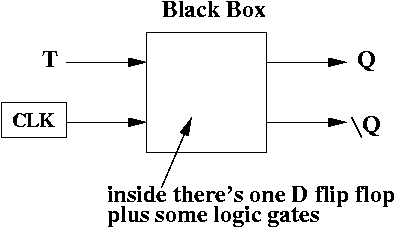
A D flip flop is as powerful as a T flip flop, if you can simulate a T flip flop. That is, feed in T and a clock into a black box, and out comes Q and \Q. The black box can only contain one D flip flop, plus some logic gates.
A T flip flop is as powerful as a D flip flop, if you can simulate a D flip flop. That is, feed in D and a clock into a black box, and out comes Q and \Q. The black box can only contain one T flip flop, plus some logic gates.
That is, they're equally powerful, if one T flip (plus logic gates) can simulate one D flip flop, and one D flip flop (plus logic gates) can simulate one T flip flop.
Here's a diagram to illustrate what's I mean:

You can also swap T and D.
You might ponder "How can I do this?" and play around with gates and trying to get the behavior correct.
However, an elegant solution turns out to be an unusual one.
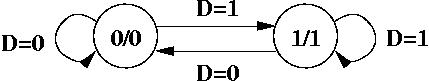
If you are in state 0, that means the D flip flop outputs a 0. If you are in state 1, that means the D flip flop outputs a 1.
D is an input to the Moore machine.
If you are in state 0, and D=1 (set operation), then you go into state 1. If D=0 (reset operation), you stay in state 0.
If you are in state 1, and D=1 (set operation), then you stay in state 1. If D=0 (reset operation), you transition to state 0.
This Moore machine has two states. We need ceil( lg ( 2 ) ) = 1 flip flop. We can either pick a D flip flop, or more interestingly, a T flip flop.
Since you've already read about how to implement a finite state machine, you can use that to implement the above Moore machine with a T flip flop.
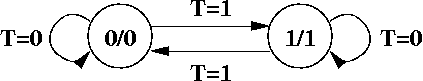
With 2 states, you just need one flip flop, and you can pick a D flip flop.
Since there are 2 bits for inputs, each state has 4 outgoing edges. It appears in the diagram below, that there are only two outgoing edges per state, but that's because each edge has two labels. There should be one edge per label, so each edge that has two labels is really two edges (but just neater, even though inaccurate, to draw one).
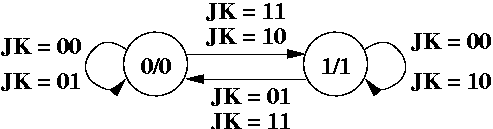
In a JK flip flop, JK = 00 is hold, JK = 01 is reset, JK = 10 is set, and JK = 11 is toggle.
As you can see, it's a combination of a D and T flip flop. However, it's no more powerful than either flip flop. As you can see from the diagram above, it's only two states, so it requires only one flip flop, and you can pick either a D or T flip flop.
We define equivalence of flip flops as saying X is equivalent to Y (where X and Y are a flip flop) if you can implement the behavior of a single X flip flop using a single Y flip flop (plus logic gates) and vice versa.
The insight is to model each kind of flip flop as two-state Moore machines. We know that two states only requires one flip flop, which we can pick. Since we already know how to implement Moore machine, we just follow those steps. Thus, we can implement the behavior of a T flip flop with a single D flip flop, and vice versa.