What's a Clock?

Background

When you buy a computer, one of the first things you probably look for is the speed of the computer. These days, it's not unusual to here rates as fast as 3 GHz.

But what is 3 Ghz referring to? This is referring to the clock rate.

The clock on a computer is not the same as the clock on the wall, which is used to tell time. A computer clock is more like a metronome, which keeps the beat for musicians to play music.

A Plot of a Clock

One way to understand a clock is to look at a plot of its behavior.

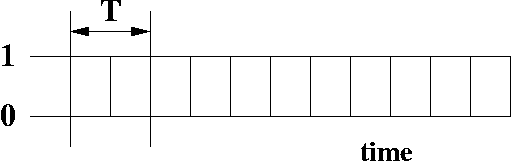
A clock changes its value from 0 to 1 every period. We use the letter T to designate the period. This signal repeats over and over again. Perhaps you remember, from a course in calculus, about sine waves. This wave repeats once per period. The difference between a sine wave and a clock is that a sine wave is curved. It gradually increases than decreases.

A clock's signal is squarish in shape.

Related to the period of the clock is the frequency. Frequency is defined as 1/T, and has units of s^-1.

When you hear clock rates, it's usually given by its frequencies. Thus, 2 Ghz means 2 x 10⁹ cycles per second. A cycle is a signal for a single period. The period for this clock is 1/2 x 10⁹ which is 5 x 10^-10 seconds, which is half a nanosecond, which is a really, really short period of time.

To give you an idea of how short this time is. Imagine that everyone in the world sang exactly one note, and exactly one person sings at a time. Suppose each note lasts one nanosecond. It would take 6 seconds to complete (assuming 6 billion people in the world).

A More Realistic Clock

A clock can't really instantaneously go from 0 to 1 and back to 0. A more realistic diagram looks like:

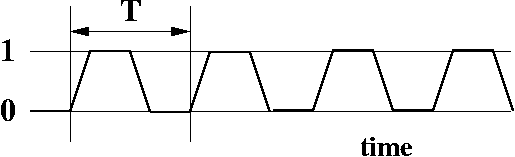
As you can see the clock signal has a positive slope from 0 to 1 and a negative slope from 1 to 0. This slope has been exaggerated so you can see it better. Normally, it wouldn't be quite so angled.

Features of a Clock

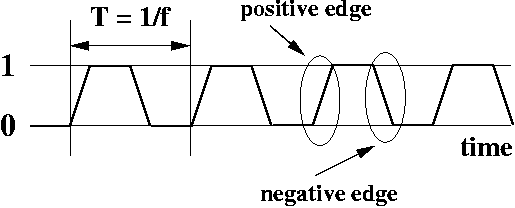
There are a few key features of a clock:

• period This is the time it takes for a clock signal to repeat. Its unit of measurement is seconds. The symbol for the period is T.
• frequency Frequency is 1/T. The unit of measurement is s^-1, which is inverse seconds. This is also sometimes called Hertz (abbreviated Hz). Sometimes people say "cycles per second" instead of Hz or s^-1. They all mean the same. When people refer to the "speed" of a CPU, they are usually talking about the clock frequency.
• positive edge When the signal transitions from 0 to 1. It's circled above.
• negative edge When the signal transitions from 1 to 0. It's circled above.

Each positive clock edge appears once per clock period. Each negative clock edge appears once per clock period.

Is It Always 50-50?

In the clock diagrams above, the amount of time the clock is at 1 appears to be T/2 (i.e., half the period). The amount of time the clock is at 0 also appears to be T/2. (There is a little time when it transitions from 0 to 1 or from 1 to 0, but let's assume this is a fairly small fraction of T).

Must a clock always do this? The answer is no. We could have a clock where it stays 1 for 3T/4 (three quarters of a period) and 0 for T/4 (one quarter of a period), or any fraction x and T - x where x < T.

If you're only using the positive edge, then it doesn't matter how long the signal stays at 1 or 0, since you only use the edge. However, if you want to use both positive and negative edges, then you're going to have to consider when you want the edges to occur.

A Simple Exercise

In order to get a feel for how a clock signal behaves, put your finger at the beginning of the clock signal in the diagram above. At this point, the signal should have a value of 0.

Begin to move your finger to the right, but trace out the signal. Your finger should move from 0 to 1, and back again.

If you happen to trace over the positive edge once a second, and you're steadily moving to the right (not going faster or slower) then the period is 1 second, and the frequency is 1 Hz.

Tracing the signal with your hand gives you a better "feel" for how a continuous signal behaves. Usually, computer science majors have a more difficult time with this (unless you really like calculus or are in engineering) because we deal with quantities that are discrete, rather than continuous.

At any point in time, someone can ask you the current value of the signal.

If we use the "pipe" analogy, we can think of this signal alternating between pumping red soda (for 0) and green soda (for 1).

What's a Clock Used For?

We use a clock to synchronize the events of a CPU. Devices in a CPU can be categorized as sequential circuits or combinational circuits. Sequential logic devices use a clock. Basically, sequential logic devices can only change outputs once a period, usually during a positive or a negative edge. We'll assume that a sequential device can only change outputs on positive clock edges.

To give you an analogy, imagine a music conductor tapping a beat with a baton (a stick) at regular intervals. Suppose you are playing a piano, and you're told to play a new note each time he taps his baton. Thus, how fast the conductor taps the baton controls how often you play notes.

Similarly, the rate at which the positive clock edge appears controls how fast a sequential logic device can change outputs.

It turns out that by using a clock, we can design a CPU more easily than if we don't use a clock. This is primary reason to use a clock.

Can't We Make It Faster?

If a CPU will run faster with a faster clock, then why not run it faster? The problem is that it takes time for signals to move around in a circuit. You can reduce this time in several ways. The main way is simply to make the circuit smaller. When the circuit is smaller, signals have less distance to travel, and therefore everything can happen more quickly.

Web Accessibility