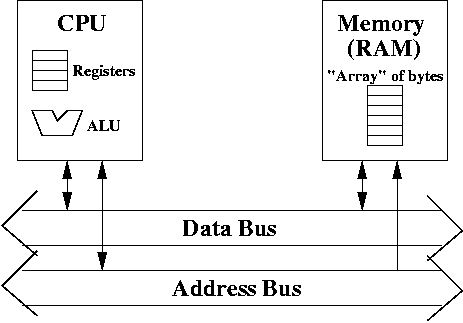

In particular, RISC machines became popular. Even though Intel processors dominate the market, they use a lot of RISC ideas. Recall that RISC machine have the following features:
Basically, in RISC, some complex instructions were eliminated in favor of running several simpler instructions that did the same task. Initially, RISC used as few instructions as they could get away with. Some academic ISAs had only about a dozen instructions.
Over time, people realized this was not a reasonable way to develop an ISA. The decision about which instructions to keep and which instructions to get rid of were based on benchmark programs. If simulations showed that including an instruction in the ISA would improve performance (speed) in many typical programs (i.e., benchmarks), then the instruction was kept in the ISA. Otherwise, it was discarded.
As a result, a typical RISC program might contain many more instructions than its equivalent CISC program, since it may take more RISC instructions to run the equivalent CISC code. (Admittedly, it was expected that this would happen infrequently).
How can RISC programs possibly be faster? How can running more RISC instructions be faster than running fewer CISC instructions? Several ways. First, if you design a CPU that has a small set of instructions, then it's easier to design and optimize the hardware. You can then run the CPU at a faster clock rate.
The CPU may run more instructions, but each instruction will run quicker because of the higher clock rate. The hope is that the slowdown from executing more instructions is more than offset by running each instruction more quickly.
Second, some CISC instructions run in many clock cycles. For example, it may take many clock cycles to run an integer divide. CISC instructions may not always run in one clock cycle, while most RISC instructions attempt to run in one clock cycle (it doesn't always succeed either, but it succeeds more often than for CISC instructions).
Third, if RISC is to be successful, then memory has to be cheap and quick. A bigger program uses up more memory, and you need to be able to access instructions that must faster. It's not surprising that RISC became a viable way to design a CPU when memory costs started to decline. When memory was expensive, the key consideration was to keep total program lengths as short as could be managed, even if it meant the instructions took longer to execute on the CPU.
Even cheap memory is not enough. Memory (RAM) is often the bottleneck when executing code. This is an important fact to remember. You may have, say, 2 GHz machines, but typical RAM can not retrieve instructions from memory at that speed.
A solution is to use small, but fast memories. For example, accessing registers is very quick, while accessing RAM is comparatively slow. This suggests that if we want speed, we need more registers, and hope that most data stays in the registers, and that we rarely need to access RAM.
This is not a reasonable assumption. Registers simply don't hold enough memory.
However, if we can use small, fast memory---this is going to be called cache, then this memory is faster than RAM, but slower than registers, and we can keep the most commonly used data (or instructions) in the cache. There's going to more data in cache (typically 512 K or so) than in registers (typically, 128 bytes).
There's a basic principle about memory. If you want lots of memory, it will be cheap (i.e., it doesn't cost much) and it's slow (to access data). If you want very fast memory, it will be small (i.e., hold little data) and expensive (per byte of memory). Historically, there used to be two levels in the memory hierarchy: registers (very fast, but very few of them) and RAM (slow, but lots of it).
In the last 20 years or so (since about 1990), cache has become increasingly important. It lies between registers and physical memory in terms of size and speed. From slowest to fastest: disk, RAM, cache, registers. Each one is faster, yet smaller.
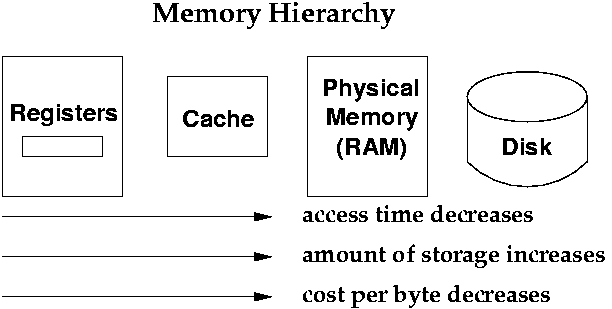
On the left are registers. They give you the fastest access time. Currently, access times for a register is about
You have a computer on your desk, and get your books online. You can download only so many books because your computer is limited in memory. The advantage of downloading the books onto your own computer is so that you can access the material quickly. Downloading the books is quite slow, so you hope not to do it very often.
If it weren't for the fact that you collect related books and write on those books for each chapter (say, 10 books on Greek mythology, then 10 books on Norse mythology), you might be forever downloading books. Even though the majority of books remain at the central library site, the books you need are on your computer, which is quick to access.
What happens if you have already downloaded 10 books (assuming they all take the same amount of space), and you want an 11th book? You will need to delete one of your books off your computer, to make room for the next book.
Which one should you pick? You could pick the one that you haven't read in the longest time. That policy is called "least recently used". Or you could see which book you've had on your computer the longest time. That policy is called "first in first out". Or perhaps the one you've looked at least. That's called "least frequently used".
In any case, you use some policy to decide which book to get rid of to make space for the new book.
Let's assume your computer can still store 10 books. There are two sites you can access books. However, there's the "Virtual Central Library" (VCL), which has any book that you might want. There's also a "Local Library" (LL).
Whenever you want to access a book, you will look in the Local Library (LL) first. If it's at the LL, you will copy the book to your own computer. If it's not there, the LL will contact the Virtual Central Library (VCL). The LL will copy the book to its own library (possibly removing a book from the LL to make space), and then you will copy the book from the LL to your own computer.
The LL is much smaller than the VCL, but can store more books than you can on your computer.
Thus, the LL serves as a "middle man". If the book you want is in the LL, you access it much faster than if you have to download it from the Virtual Central Library (VCL). For example, let's say it takes 1 second to access the LL, and 100 seconds to access the VCL.
However, when you are unable to find the book in the LL, you spend 100 seconds getting a copy from the VCL to the LL, and one more second to get it from the LL to your local computer. Thus, it's actually slower to use the LL (not by much) if the book you're looking for is not there. This is where we get a more accurate representation for cache.
Cache works very similarly. Basically, you want some data (or an instruction) at some address. This data either appears in the cache (which is like the LL) or it isn't. If it's not there, you need to access the data from RAM (which is like the VCL). This data is then copied to the cache, and then from the cache to the registers. Thus, the registers act like your local computer.
In fact, cache has become so useful, most modern CPUS often have two levels of cache. They are called L1 and L2 caches for level 1 and level 2 cache.
Here's how to visualize an L2 cache. Imagine a "State Library" (SL), which is bigger than the LL, but smaller than the VCL.
Every book in the LL is in the State Library (SL). However, the SL has more books than the LL. Every book the SL is also in the VCL. Thus, LL is a subset of SL, which is a subset of VCL.
To access a book, you go to the LL. If it's not there, you check the SL. If it's not there, you go to the VCL. That data gets copied to the SL, then back to the LL, and finally to your computer.
In principle, you can carry this idea of caching many, many levels.
Each level is a subset of the next level. The higher the level, the more memory, and the slower it gets. For example, we could label the levels of memory as L1, L2, L3, etc. where all the data in level Li is a subset of that in level Li+1.
When you look for data at a particular address, you search for it at the smallest level, and if you can't find it there, you look at the next level. Once you find the data you are looking for, you copy it down to the lower levels, possibly getting rid of a cache line in the process.
Definition A cache line is the "unit" of data you transfer to a cache. Typically, this number is a power of 2 (say, at least, 16 bytes).
For example, suppose you visit a particular webpage at a website. Initially, that webpage may be slow to download. But, when you visit another webpage and come back, it seems much faster "download" the old webpage. Why is that?
A local copy of the webpage is kept on your computer. Thus, your computer's hard drive (or possibly memory) is being used as a cache for that webpage. This can sometimes create problem, especially if the content of the webpage is always being updated (sports scores for a live games, for example).
These days, hard disks also have memory that serves as cache. Recall that hard disks are used to store files. Recall that hard disks are also slow. So, one idea is to use RAM as a cache for the disk. As files are accessed, place it in a special RAM just for files. When you want to edit a file, you check in the file RAM first, and if it's not there, then you check on the disk. This is done automatically for you, via the operating system.
As you can see, the principle of caching is simple. Use faster memory to store frequently accessed data.
The memory hierarchy wouldn't be very effective if two facts about programs weren't true. Programs exhibit spatial locality and temporal locality.
Do programs exhibit spatial locality? Yes, they do. For example, when you accessing data from arrays, you are accessing memory locations that are contiguous. Also, instructions usually run sequentially (with the occasionaly branch or jump). Since instructions are contiguous in memory, they exhibit spatial locality. When you run one instruction, you're likely to run the next one too. That's the nature of running programs.
This happens when you run code in a loop. You access the same instructions over and over. If you process an array in a loop (say, bubble sorting), then you access array elments over and over again too.
Each time you download a book, you would look in the local library. Assuming it's random, the probabilty that the book is in the LL would be low (since it stores only a small subset of the VCL). So you would have to go to the Virtual Central Library to find the book. Since accessing the VCL is very slow, you pay a fairly large cost (in time) for accessing books.
Furthermore, you have to copy that book from the VCL to the LL too. We copy the book to the LL, so it can be cached, and accessed again in the near future. However, since you're accessing books randomly, the books in the LL won't be used in the near future, and you will always have to access the VCL.
In effect, the LL is useless to you.
You get benefit from using the Local Library if you're accessing the books found in the LL all the time. When you search for the same books over and over, they appear in the LL, and access time is much smaller to access the LL than the VCL.
To apply the analogy to hardware, if you want to to access data and it's found in cache, you get savings in access time, since accessing data (or instructions) found in the cache is much quicker than accessing main memory, all the time.
On the other hand, if you don't access data in the cache very often, then the cache is not useful, and may in fact, cause a small delay than not having the cache at all.
What about spatial locality? This says that if you access address X, you are like to access addresses near X too.
Spatial locality suggests the following strategy when accessing data. Load the data from many contiguous addresses near X from RAM into the cache. That is, copy a block of data from memory to cache. This block should be larger than 4 bytes which is the typical amount you would access from RAM to registers.
This idea wouldn't be so great if it weren't quicker to access the entire block at once, as opposed to accessing the bytes one at a time. This makes some sense if you think about it. Suppose you were ordering books. If ordering 10 books at once took just as much time as ordering each book individually, then there's no need to order 10 books at a time. Just order them whenever you want them. (There's price----i.e., you might save money if you order 10 books at once, but there's no real analogy to price for hardware).
However, this turns out to be inconvenient. It's easier to access the data in the following way.
Suppose we want to copy a data block of 32 bytes from memory (instead of just 1 or 4 bytes). We need 5 bits to specify each of the 32 bits. Thus, 00000 is byte 0, and 11111 is byte 31.
Suppose you want to access address A31-0. Instead of accessing only that single address, generate the following 32 addresses:
That is, take the upper 27 bits of the address. Concatenate that with all possible 5 bit bitstrings (there are 32 such bitstrings).
This creates 32 consecutive addresses. Copy the data in those addresses from RAM to the cache. That data is called the cache line.
To see if you understand what's going on, how would you create the addresses if you wish to copy 64 bytes in a cache line.
Instead of using the upper 27 bits, you now use the upper 26 bits. You then create all possible 6-bit bitstrings (there are 64 of those) and concatenate them to the 26 bits. This creates 64 addresses in memory. Copy the 64 bytes from main memory to the cache.
We will give the upper 27 bits a name. We will call it the tag. Thus, when you have 32 bytes, you know exactly where they come from in memory, if you know the tag.
When we copy the 32 bytes, we place them in the cache in the same order they appear in memory. We can imagine that data being stored in an array with indexes 00000 up to 11111. (There are 32 elements in this array, which should not be so surprising, since that's how much we copied).
If we want to access address A31-5 00011, then we look at index 00011 of the "array", to get the data.
00011 is considered the offset into the array.
Given the tag and the offset, we know what address the data at a given offset is. For example, if we access the data at 00011, then this data is the same as the one at the address given by the tag concatenated with 00011, i.e., address A31-5 00011.
A slot consists of the following:
The total amount of memory used in a slot that stores 32 bytes in a cache line can be easily computed. There's 2 bits (one for V and D), plus the tag (27 bits), plus the data in the cache line (32 x 1 byte = 32 bytes = 256 bits). That's a total of 285 bits.
Here's a diagram of one slot.
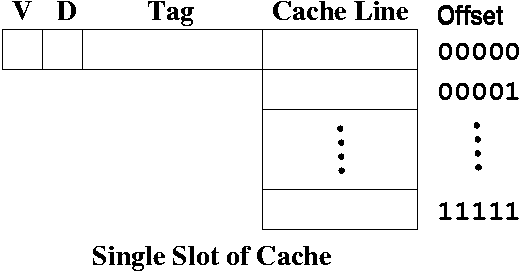
There's variation to the slot, which we'll discuss when we talk about direct mapped cache, and set associative cache.
You want to maximize cache hits, because then you have much improved performance (speed).
You look for the address to see if it's one of the addresses in cache. If the address (and its contents) are NOT in the cache, then you must access it from main memory. This means that you must copy the data from memory to the cache.
Since the cache is a small subset of main memory, there may be data that you need to remove from the cache (just as you had to remove books from your computer, if you needed other books to replace it).
Thus, it's rather common to have two caches: an instruction cache that only stores instructions, and a data cache that only stores data.
You see some indication of this in the CPU design where there's "instruction memory" and "data memory".
There are two ways to do this:
This approach creates an inconsistency between cache and memory. Cache has one view of memory (which is accurate), while main memory does not have the latest updates.
Normally, this is not a problem. After all, there's only one CPU, so who else would need to access memory? However, if you had more than one CPU, each with their own cache, this problem of memory consistency becomes a much bigger issue. A CPU accessing memory may not have the latest update, because another CPU has modified a memory location, but the update is only in the cache.
Write-back is convenient because you don't have to access main memory, which can be slow.
The disadvantage occurs when there are many writes to memory. This can cause a backlog waiting for the writes to occur.
The advantage of write-through is that you don't have to worry about memory consistency, since cache and memory should have the same values (even though it may take memory a little longer to get the correct value).
Which slot should you pick? There are many policies. Any will do. Here's a list:
These policies often require additional hardware to indicate time of use or frequency of use. There have also been other fancier schemes to decide how to get rid of a slot.
When you choose a slot to be evicted, you look at the dirty bit (we assume a write-back policy). If D = 1, i.e., the slot is dirty, then copy the cache line back into memory. Otherwise, you can overwrite the cache line with the new data, tag, etc.
When the new cache line enters,
This is convenient, because the cache scheme can be changed without having to modify any programs. Often, there's a question as to how much the actual implementation (called the ISP, the instruction set processor) should be visible to the ISA programmer. The more that's visible, the more that you restrict the implementation, and the fewer chances for optimization.
Thus, you only want to reveal just enough of the real hardware for programmers to get the job done, and no more. In effect, the ISA is a kind of specification for the actual CPU, which can be implemented in one of many ways.
Super word-aligned means that if you have 2k consecutive bytes, the first byte must reside at an address divisible by 2k. Thus, if the cache line has 16 bytes, it must be at an address divisible by 16, which means it's automatially word-aligned (since word-aligned means divisible by 4).
You'll never have half a word in one cache line, and the other half in another cache line (provided the cache line contains at least 4 bytes) as long as the word is word-aligned.
To convince yourself of this, try to have a word that is word-aligned, and see if you can create a cache line where only part of the word is within it.
If you can do it, more than likely, you have misunderstood how cache lines work.
When data at an address is needed, the CPU first searches in the cache. If it finds it there, then a load or store is performed to or from a register.
If a cache miss occurs, then a cache line needs to be copied from main memory to a slot in a cache, which may require the eviction of a slot.
Ideally, you want the percentage of cache hits to be high, to give the illusion that all the useful data is in the cache, and being accessed at the speed of the cache, as opposed to the speed of main memory. How effective this is depends on how much spatial and temporal locality the particular program being run has.