How to Convert From Base 10 to Base K

Converting numbers from base 10 to a different base (we'll call it base K) is harder than converting it to base 10. We used a summation formula to convert from base K to base 10. This involved multiplication and addition.

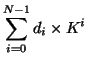
To convert a number to a different base, we're going to use division.

I'll present the algorithm right now, then explain the intuition behind it.

Algorithm

Here's the pseudocode for converting from base 10 to base K

   // num stores a value in base 10
   // solution will have digits in an array
   index = 0 ;
   while ( num != 0 )
    {
       remainder = num % K ;  // assume K > 1
       num       = num / K ;  // integer division
       digit[ index ] = remainder ;
       index ++ ;
    }

The Intuition

In the previous set of notes, we wrote a table that looked something like the following:

d₃	d₂	d₁	d₀
2³	2²	2¹	2⁰
-	-	-	-

We're looking at a potential 4-bit base 2 value. I say "potential" because I haven't filled in any of the 0's and 1's yet.

My goal is to represent the number 13₁₀ in binary (i.e., in base 2).

I'm going to fill them in a way that's invalid, but bear along, because it'll help you understand the algorithm above.

d₃	d₂	d₁	d₀
2³	2²	2¹	2⁰
0	0	0	13₁₀

To make this easier to understand, imagine that you've gone on vacation to some other country. This country uses dollar bills too, but instead of using 1 dollar bills, 5 dollar bills, 10 dollar bills, etc., this country uses denominations that are powers of 2. Thus, there's a 1 dollar bill, a 2 dollar bill, a 4 unit bill, and so forth.

You wish to exchange 13 US dollars in this new currency. Futhermore, you want to get as few bills as possible (perhaps they charge a smaller fee when this happens).

Initially, however, we start of with the d₀ position having the value 13. That's equivalent to 13 1-dollar bills. However, from the previous set of notes, you know that in base 2, each bit position can only have a value between 0 and 1, inclusive. It's not valid to have 13 in d₀ (plus, it doesn't minimize the number of bills).

But, for now, let's pretend that it is OK to have it there. What value would we get if we applied the summation formula (where K=2, since this is base 2)?

If we apply the summation, we get:

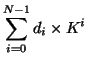
   13 * 2⁰ = 13 * 1
           = 13

Of course, this makes sense. We put 13 in the 2⁰ position. That's the same thing as saying, we want 13 one-dollar bills. Surely, that adds to 13.

Still, we have this problem that we can't really put 13 in that position.

To fix this problem, we're going to divide 13 by the base. In this case, the base is 2, so we'll divide 13 by 2. Thus, 13/2 = 6. Think of dividing by 2 as a way of counting how many 2-dollar bills we'll need. Dividing by 2 is equivalent to finding how many groups of 2 we have. In this case, after dividing, we have 6 pairs. Of course, there's still one left over. That's the remainder, which is 1.

We can rewrite, in our chart, as:

d₃	d₂	d₁	d₀
2³	2²	2¹	2⁰
0	0	6₁₀	1₁₀

This means, we have 6 2-dollar bills, and 1 1-dollar bill.

This time, d₀ has a value between 0 and 1 (as it should), but d₁ = 6. d₀ has a valid bit value, but d₁ doesn't.

Nevertheless, the summation still works.

  (6 * 2¹) + (1 * 2⁰) = 13 * 1
                      = 13

Essentially, this says we have six 2-dollar bills and 1 1-dollar bill, which still adds up to 13 dollars. The total is still correct.

Still, we have violated the rule which says that no digit in base 2 should be greater than 1. Currently, there's a 6 at d₁ position. What to do now?

We divide d₁ by 2. Intuitively, we're trying to take the 6 two-dollar bills, make pairs of two-dollar bills, so we can exchange them for 4-dollar bills. Recall that dividing by 2 is equivalent to counting how many pairs you have. So, when you divide 6 by 2, you're trying to count how many groups of 2 you have. If you were dividing by, say 3, you're trying to count how many groups of 3 you have. (Thus, 13/3 = 3, so you have 3 groups of 3, with 2 leftover).

d₃	d₂	d₁	d₀
2³	2²	2¹	2⁰
0	3₁₀	0	1₁₀

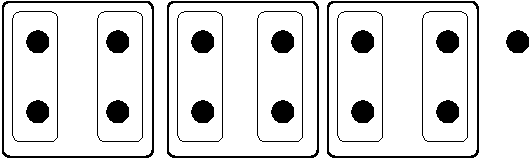
We can think of this in a different way. Let each dot below represent a dollar bill.

There are 13 (rather large) dots above. When we divide by 2, we create 6 groups of 2. Those groups of 2 can be exchanged for 5 two-dollar bills. We can then take these two-dollar bills and divide by 2 again. This leaves us with 3 two-dollar bills (this is shown by grouping them in 4 dots).

When you divide 6 by 2, this creates 3 groups of 4. The chart shows that d₂=3. This is invalid. Again, the trick is to divide by 2 and exchange 4 dollar bills with 8 dollar bills.

3 / 2 = 1, with a remainder of 3. That means, we can take our 3 4-dollar bills, and create 1 pair of 4-dollar bill, and exchange it for 1 8-dollar bill. However, because there is a remainder of of 1, that means we have a 4-dollar bill left over.

If you use the diagram above, the goal is to make groups of 8 from two groups of 4. You can make one group of 8, but have one group of 4 left over.

d₃	d₂	d₁	d₀
2³	2²	2¹	2⁰
1₁₀	1₁₀	0	1₁₀

At this point, we can basically stop. We place the 1 in the d₃ position (which is the 8's place). The remainder is in the d₂. Both are valid values.

Thus, 13₁₀ = 1101₂. You can verify this is correct by converting 1101₂ back to base 10.

Revisiting the Algorithm

The algorithm does more work than we do. Basically, the algorithm repeatedly divides by the base (in the previous example, the base is 2). It sets the remainder in the digit position.

Let's trace this out (Look back at the algorithm at the top).

Let index=0.
Divide 13 by 2. This is 6 with a remainder of 1. So, we store the remainder in the array, i.e., d[index]=1 where index=0. Basically, we're means that d₀=1.
Increment index to 1, and go back to to of loop.
Since 6 is not 0, we again divide by 2. This is 3, with a remainder of 0. We store the remainder in the array, i.e., d[index]=0 where index=1. Equivalently, d₁=0.
Increment index to 2, and go back to to of loop.
Since 3 is not 0, we again divide by 2. This is 1, with a remainder of 1. We store the remainder in the array, i.e., d[index]=1 where index=2. Equivalently, d₂=1.
Increment index to 3, and go back to to of loop.
Since 1 is not 0, we again divide by 2. This is 0, with a remainder of 1. We store the remainder in the array, i.e., d[index]=1 where index=3. Equivalently, d₃=1.
Increment index to 4, and go back to to of loop.
At this point, our value is 0, so we're done.

The only tricky part of the algorithm is when you deal with bases greater than 10. Each array element is really storing an integer. Thus, when you are working in base 16, say, you might be storing the value 12 in one of the elements.

To convert it to base 16, you typically create a string. You convert each element to a character (or a string of one character). If the array element contains a value from 0 to 9, you convert it from "0" to "9". If the value contains a value 10 or greater, you convert it to "A" and above. Obviously, you run into problems if you are using bases higher than 36, but for now, assume you aren't.

An Alternate Approach

The algorithm described is basically how you would convert a number, if you had to write a program. However, it can be intuitively difficult to think about.

Here's an alternate algorithm, that works well if you're working in binary. It doesn't work well for other bases.

   pow = getLargestPowerOfTwo( num ) ;
   val = power( 2, pow ) ; // compute 2^pow
   while ( val != 0 )
     {
        if ( num - val >= 0 ) 
           {
              num -= val ;
              digit[ pow ] = 1 ;
           }
         else
            digit[ pow ] = 0 ;
         pow-- ;
         val /= 2 ;
     }

Let's convert 13 to base 2.

For base 2, pick the greatest power of 2 that is less than or equal to the number you're converting. That is, find the largest N, such that 13 >= 2^N.

The greatest power of 2 less than or equal to 13 is 8. 8 is 2³ and corresponds to d₃.

Subtract the value, but only if the result is 0 or positive. So, 8 subtracted from 13 is 3, which is positive. Place a 1 in d₃.

Now, divide 8 by 2 (we're considering d₂). This results in 4. Try to subtract 4 from 3. You get -1. So don't subtract. Since it's negative, place a 0 in d₂.

Now, divide 4 by 2 (we're considering d₁). This results in 2. Try to subtract 2 from 3. You get 1. So subtract. Since it's non-negative, place a 1 in d₁.

Now, divide 2 by 2 (we're considering d₁). This results in 1. Try to subtract 1 from 1. You get 1. So subtract. Since it's non-negative, place a 1 in d₀. Since we're at d₀, we're done.

This technique doesn't really work for other bases, but can be modified to do so. The original algorithm presented is easier if you want to work in bases other than 2.

Summary

Converting a number to base K involves repeatedly dividing by K, and storing the remainder in an array. You can then take the values out of the array and create a string that looks like the printed form of that number.

What are you really doing when you divide by K? Essentially, you are trying to create larger and larger powers of K. Notice that the remainder, when dividing by K, is between 0 and K - 1. This is exactly the property we want when we convert to base K.

As practice, pick an arbitrary number in base 10, and convert it to an arbitrary base. To double check your answer, convert it back to base 10 to see if you get the same number as before.

Web Accessibility