ROM trick: Implemeting Truth Tables with Multiple Outputs

Introduction

An extension to the MUX trick is the ROM trick. It's convenient to show the ROM trick, even though a ROM is not a combinational logic circuit. A combinational logic circuit does not have memory, while a ROM, by its very name, does. Nevertheless, the "trick" is similar, so it's worth looking at.

Read-only memories allow you to read, but not modify the memory. The idea is to initialize the memory once, and then use it as a kind of lookup table from that point onward. ROMs can be used as a kind of control unit, but we'll not discuss that right now.

Some ROMs are programmable multiple times. For example, an EPROM is short for an erasable programmable read-only memory. You can erase the contents of the EPROM, typically, by exposing it to ultraviolet light, then "burning" the new contents in. EEPROM are short for electrically erasable programmable read-only memory. Electrical currents can be used to erase the contents (making it easier to reprogram).

RAM (random access memory) often needs a refresh current to keep the contents of memory active, while ROM can often retain the contents even when power is removed.

Think of ROMs as an extension to the MUX trick.

Example: Implementing Carry Out and Sum

Full adders have two outputs: carry out and sum. Here's the truth table for a full adder.

Row	x	y	c_in	c_out	s
0	0	0	0	0	0
1	0	0	1	0	1
2	0	1	0	0	1
3	0	1	1	1	0
4	1	0	0	0	1
5	1	0	1	1	0
6	1	1	0	1	0
7	1	1	1	1	1

Let's implement both c_out and sum.

To do so, we use an 8-1 2-bit ROM. Each address of ROM contains a 2-bit quantity. Unlike the MUX, the bits are stored inside the ROM itself. Thus, a ROM is not a combinational logic circuit, since combinational logic circuits do not have memory.

In general, memory circuits are slower than combinational logic circuits.

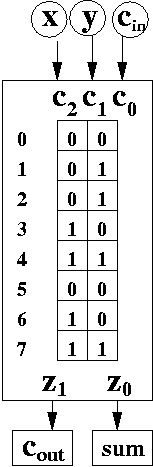
Let's look at the ROM above. The ROM has 3 address bits c₂c₁c₀ which we still call control bits. This allows us to pick one of 8 possible addresses. Each address (for this ROM) stores 2 bits. We can imagine ROMs storing any number of bits at each address, not just 2 bits, as shown above.

Suppose c₂c₁c₀ = 100. This selects address 4. In the example above, address 4 contains the two bit quantity 11. This quantity is then output as z₁ z₀ at the bottom of the ROM.

We can use ROMs very much like we use MUXes. They can be used to implement truth tables. There are differences between the two. The MUX use hardwired 0's and 1's which come from outside the MUX, and are fed into the inputs. By contrast, the ROM stores the information inside the ROM itself. Thus, you see 16 bits of memory in the ROM (8 addresses, with 2 bits per address).

Let's see how this ROM implements the full adder, whose truth table was given above.. Look at the address bits c₂c₁c₀ = 001. In the ROM example shown above, that address contains bits 01. Why did we put 01 at that address?

01 also corresponds to the two bits of row 1 in the full adder truth table above. If you look at that row, c_out = 0 and sum = 1. Thus, for each row of the truth table, we copy the outputs bits to the corresponding address in the ROM. Thus, the output bits row 0 are copied to the bits of address 0. The output bits of row 1 from the truth table are copied to the bits of the ROM at address 1, and so on for all 8 addresses.

It's easy to make a ROM output a truth table with multiple outputs.

Pick an N-bit address ROM where 2^N is the number of rows.
In each memory element, copy the output bits corresponding to the rows. For example, in the full adder, the two bits on row 1 are 01. Copy 01 to address 1 of the ROM. Do the same for each row.

Is This Really a Good Idea?

The ROM trick is, again, more of a trick then a good idea. It allows you to implement a truth table with more than one output quickly. If a ROM stores k bits per address, than you can create an equivalent circuit using k MUXes.

The point of the trick is to allow you to implement circuits quickly in exam situations.

Web Accessibility