MUX trick: Implementing Truth Tables

Introduction

Someone gives you a truth table and says you can implement it with whatever gates or parts you want. How would you do it quickly?

One way to implement a truth table is to derive a sum-of-products expression. This is how it's done:

For each row with a non-zero output, create a minterm.
OR all the minterms together

The advantage of this method is that it's easy, and doesn't require much thinking. The disadvantage occurs when you have a lot of minterms. You may draw many gates.

There's a quick and dirty way to implement a truth table.

Example: Implementing Carry Out

Full adders have two outputs: carry out and sum. Here's the truth table for a full adder.

Row	x	y	c_in	c_out	s
0	0	0	0	0	0
1	0	0	1	0	1
2	0	1	0	0	1
3	0	1	1	1	0
4	1	0	0	0	1
5	1	0	1	1	0
6	1	1	0	1	0
7	1	1	1	1	1

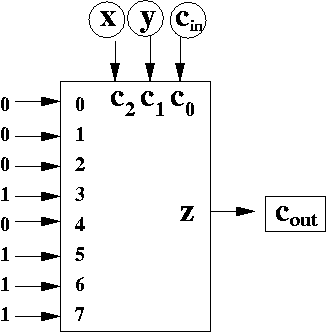
Let's implement one of the two outputs. Let's implement c_out.

To do so, we use an 8-1 MUX.

How did we create this circuit? Look at the truth table above. Look at the column with c_out. That column has the values 0, 0, 0, 1, 0, 1, 1, 1. That's also exactly the hardwired inputs being fed into the MUX, in exactly the same order.

Look at the control inputs. They are fed in with x, y, and c_in. Again, that's exactly the same order the input variables appear in the truth table.

Let's see what's happening. Consider row 5. We select row 5 when the input variables xyc_in = 101. Recall that 101 is 5 in UB.

Thus, when c₂c₁c₀ = 101, that is, when the control bits of the MUX are set to 101 (which is 5 in UB), then input x₅ is selected. In the example, above, input 5 is set to 1, which also happens to be the output of c_out when xyc_in = 101.

In a nutshell, the MUX trick is the following:

Pick an N-1 mux where N is the number of rows.
Hardwire the 0's and 1's in exactly the same order as the output.
Feed in the input variables into the control bits in the order they appear to control bits c_k-1...c₀.

Is This Really a Good Idea?

Is the MUX trick really a good idea? If you're concerned about the number of gates, it's probably not a good idea. For example, consider implementing x₃x₂x₁x₀. This would require three AND₂ gates.

However, it would require a 16-1 MUX using the MUX trick.

The reason for using the MUX trick is twofold. First, on an exam, it may allow you to answer an implementation question far quicker than using sum-of-products. At times, you use tricks to answer questions quickly, even if it's not the most "efficient" answer.

The second reason is to make you aware that MUXes can be used to implement truth tables easily, if somewhat inefficently.

Web Accessibility