Compared to an electrical engineering curriculum, we'll study digital logic design in a fraction of the time. How can we study it so quickly? Two reasons. First, we'll go over the material quicker than in an electrical engineering course. Second, we'll leave out some topics (most notably, circuit minimization and race conditions).
Just like the study of mathematical logic is done in two steps (propositional logic, followed by predicate calculus), we'll also study digital logic in two steps. First, we talk about combinational logic, then sequential logic.
I like to think of combinational logic circuits as implementations of Boolean functions. Think of Boolean functions as an abstraction, and combinational logic circuits are the implementation of that abstraction.
Of course, you can also think of combinational logic circuits as an abstraction, too, and the actual silicon as the implementation. This goes to show you that there can be many levels of abstraction, even in hardware.
We begin by discussing Boolean functions.
First, let's define the set B = {0, 1}, where B is the set of Boolean values.
Instead of using true and false, we'll use 0 (for false) and 1 (for true). While this choice may appear to be purely representational (i.e., we're using 0 and 1 as shorthand for false and true), using numerals 0 and 1 also serves a second practical purpose: we can treat the 0's and 1's as numbers in a representation system, and eventually do math with the 0's and 1's.
We define
Bk = B1 x B2 x ... x Bk
where Bi = B. This is the Cartesian cross product
of k sets.
Bk is set of all k-tuples (b1, b2, ..., bk) such that bi is either 0 or 1 for all 1 <= i <= k. A k-tuple is basically a k-dimensional coordinate.
Now that sounds mathematical doesn't it? However, you can also think of Bk as the set of all k-bit bitstrings. That should make this set much easier to understand. As you should know by now, Bk has size, 2k, since it's basically the set of all possible k-bit bitstring.
Now was can write a definition for Boolean functions.
Definition A Boolean function is Bk -> Bm, which is the set of all functions that map k bit inputs to m bit outputs, where k >= 0 and m > 0.Recall what a function is, from your discrete math courses.
A function consists of:
Usually, for each element in the domain, the mapping assigns one element of the codomain. If this happens, the function is said to be total.
Sometimes, there are some elements in a domain that are not assigned at all. Thus, the mapping for these elements are unknown. Such functions are said to be partial because not every element in the domain is mapped.
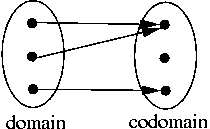
For finite domains and codomains, we can draw pictures.

Here are a few observations on the above diagram.
Bk -> Bm is the set of all functions that map k-bit bitstrings (which is the domain of a single function in the set) to m-bit bitstrings (which is the codomain of a single function in this set). Remember Bk -> Bm this is a set of functions, not one single function.
This set is quite large, as you might imagine. The total number of functions is 22km. The way we come up with this answer is based on truth tables.
Yet, fundamentally, a (mathematical) function is simply something that maps inputs to outputs. There's no need to explain how this mapping is done. Of course, in reality, we worry about how to perform this mapping using computation because it gives us a compact way to represent the mapping. Furthermore, it's also its own study. Algorithms is the study of efficient computatble functions that solve problems.
You may think "I've never seen a mapping before", but you have. Truth tables! Truth tables are one way to define a Boolean function.
Let's look at an example of a truth table. We're going to follow the following convention. Input variables start with the letter x, possibly with some numeric subscripts. Output variables start with the letter z, possibly with some numeric subscripts.
| x2 | x1 | x0 | z2 | z1 | z0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Since there are 3 input variables (i.e., 3 bits), there are 23 = 8 possible 3-bit patterns. Thus, there are 8 rows.
This truth table is a function of the following type B3 -> B3. That is, it's a function which is an element of the set of functions from 3-bit inputs to 3-bit outputs.
Let's look at the previous truth table.
| x2 | x1 | x0 | z2 | z1 | z0 |
| 0 | 0 | 0 | - | - | - |
| 0 | 0 | 1 | - | - | - |
| 0 | 1 | 0 | - | - | - |
| 0 | 1 | 1 | - | - | - |
| 1 | 0 | 0 | - | - | - |
| 1 | 0 | 1 | - | - | - |
| 1 | 1 | 0 | - | - | - |
| 1 | 1 | 1 | - | - | - |
The rows with the numbers are all possible 3-bit input values. A function maps each one of the rows to some 3-bit output value. I've replaced the outputs with dashes. Pick any combination of 0's and 1's to replace the dashes. Each combination represents a function.
The question is how many possible ways are there of filling out the dashes with 0's and 1's?
To answer this we need to count the number of dashes. This turns out to be the number of rows times the number of columns.
How many rows are there? The number of rows is 2k given k input bits. That makes sense because we are attempting to map every possible k-bit value to an m-bit value, so the total number of k-bit values is 2k.
How many columns are there? There are as many columns as bits used for the output. In this case, there are m bits used for the output.
Therefore, there are 2km slots with dashes in them. Each of those can be filled with either a 0 or a 1. So, think of all those slots as one very large bitstring. That is, a bitstring with 2km bits.
And how many possible bitstring patterns are there for n bits? There are 2n. In this case, n = 2km, so plug it in, and you get: 22km