Case Study: Implementing an 8-1 MUX

Introduction

Recall that a MUX (multiplexer) is an input selector. That is, it selects from one of N different data inputs, and directs the input selected to the output.

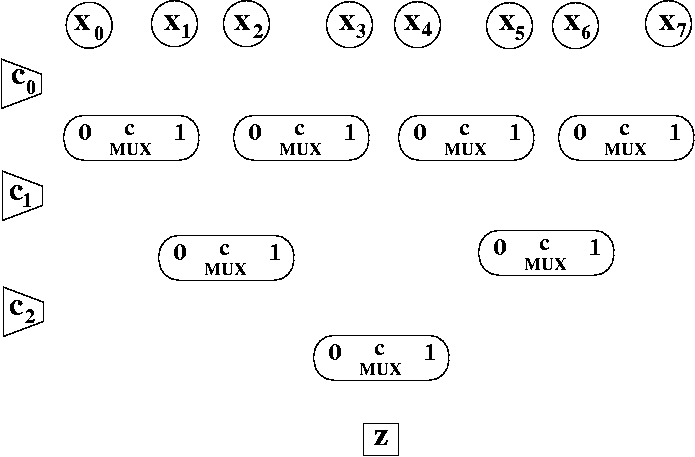
Given N data inputs, there are ceil( lg ( N ) ) control bits.

You'd think there would be nothing new to learn from implementing an 8-1 MUX from smaller MUXes that you didn't already learn from implementing a 4-1 MUX and a 5-1 MUX.

Once you see the differences between a 4-1 MUX and an 8-1 MUX, it becomes easier to handle, say, 16-1 MUXes. Usually, you need two or three related examples to see a pattern. Often, it's too difficult to see a pattern using only a single example or even two.

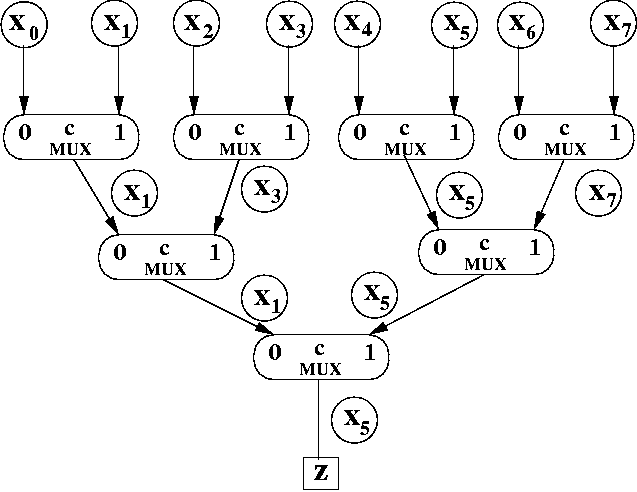
We won't specify the behavior of an 8-1 MUX using a table, since we are going to implement a standard 8-1 MUX. A standard 8-1 MUX treats the c₂c₁c₀ as a 3-bit UB number. Thus, c₂c₁c₀ = 111 selects x₇ because value_UB["111"] = 7₁₀.

Initial Setup

Here's the initial set up for implementing an 8-1 MUX. We haven't connect the data and control inputs up, nor the outputs.

Web Accessibility

Hooking it up

Then, we hook it up.

What's Going On?

You might wonder why we hooked up the 8-1 MUX as we did. Notice that the first row of MUXes' control bit comes from c₀. The second row of MUXes' control bit comes from c₁. The bottommost MUX's control bit comes from c₂.

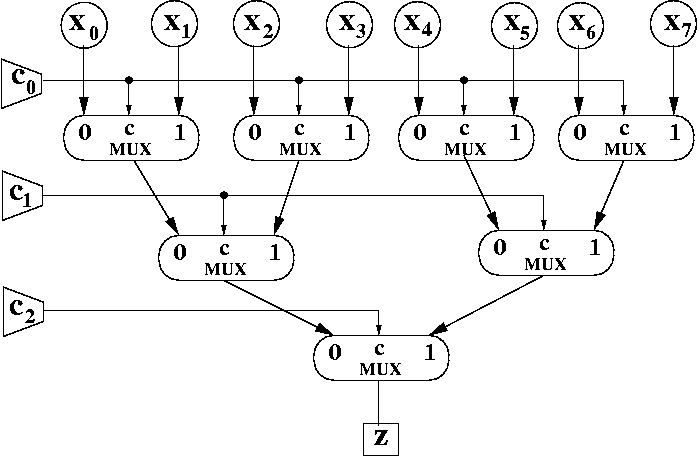
Think about an 3-bit UB number, c₂c₁c₀. What happens when you change c₀ from 0 to 1 or back? How does the base value change? It changes from being an even number to being an odd number and back, depending on the value of c₀.

How about changing the value of c₁ from 0 to 1 or back? this modifies the value by plus or minus 2. For example, if you had the 3-bit number 101, then flipping c₁ changes the value from 7_ten to 5_ten. That is, changing c₁ from 0 to 1, increases the value of the number by 2 (in UB), and changing c₁ from 1 to 0, decreases the value of the number by 2 (in UB).

Similarly, changing c₂ from 0 to 1, increases the value of the number by 4 (in UB), and changing c₂ from 1 to 0, decreases the value of the number by 4 (in UB).

Let's see how that helps us to understand what's going on. Suppose the control bits have the following value: c₂c₁c₀ = 101. This means we want to select x₅.

Let's see what happens at each step.

First Row of MUXes

The first row of MUXes is attacked to c₀ = 1. This control bit selects odd vs. even. Since c₀ = 1, it selects odd (odd numbers have their least significant bit, i.e., c₀ equal to 1).

As you can see in the diagram, this selects the inputs with odd valued subscripts.

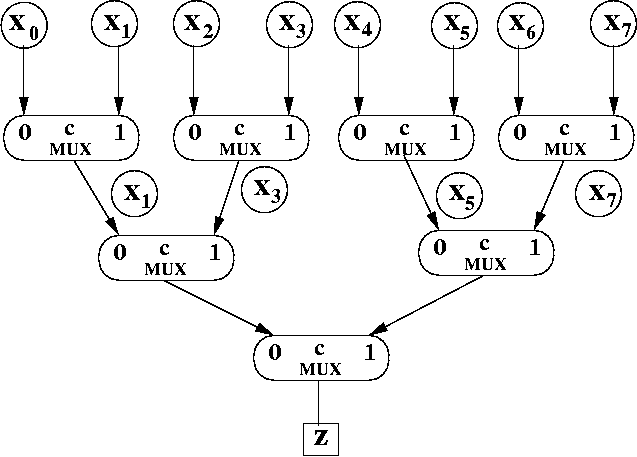
The control bits were removed to make the diagram easier to read. However, in reality, they would still be there.

Second Row of MUXes

Of the inputs that were selected by the first row of MUXes, you'll notice all of them are differ in value by 2.

Now imagine that we divide each of those indexes by 2. Instead of x₁, x₃, x₅, and x₇, we'd imagine them to be x₀, x₁, x₂, and x₃.

In that case, we'd be using control bit c₁ to decide between even and odd again. Even though we won't rewrite the index values in the diagram below, effectively, that's what's happening.

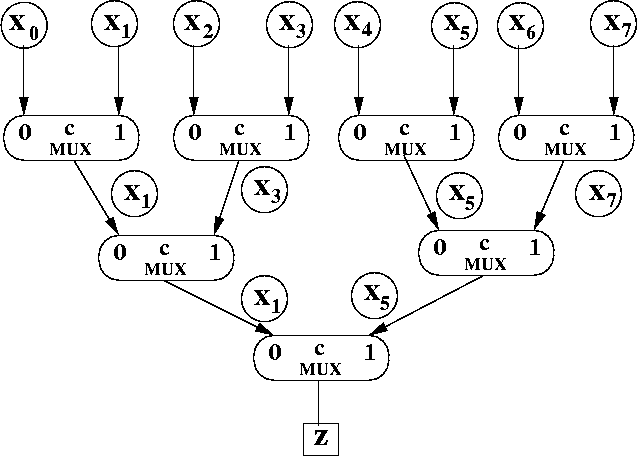
x₁ and x₅ made it past the second row of MUXes. They were the "even" indexes once you divided the index number by 2 (0 and 2).

Third Row MUX

x₁ and x₅ are the inputs of the bottom MUX. If you divide index 1 and 5 by 4, then you get 0 and 1. Then c₂ picks the even or odd index.

Since c₂ = 1 in our example, this picks x₅

Rule of Thumb

In effect each control bit selects an "even" or "odd" choice. However, we define even and odd in this way. For control bit c_i, take the index of the index that makes it to that row, and integer divide by 2_i.

The result of the integer division is either even or odd. If c_i = 1, it picks the "odd" index (i.e., input 1 of the MUX). If c_i = 0, it picks the "even" result (i.e., input 1 of the MUX).

Summary

There's a pattern to learning how to build bigger MUXes from smaller ones. However, you often have to practice on many examples to see this input. This is generally a form of "generalization". That is, trying to deduce the correct rules by analyzing many similar examples. This is one way that humans learn how the world works.

Generalization is the opposite of deduction. In deduction, you are given a formal set of deduction rules, and some facts, and you use those rules to deduce new facts. Thus, from a small number of axioms (facts), you can show many different facts (theorems).

Even though mathematics appears to be about deduction, many of the theorems came from staring at examples, and trying to create some theorem from it, and then trying to prove it works.

Right now, you've seen how 4-1, 5-1, 8-1 MUXes work. You might still discover that there are ways to tweak the MUX problem that forces you to revise your observations. Thus, certain observations that seem to work in a few examples, may not hold up as you look at different examples.